| Definitions | t  T, T,  x:A. B(x), P x:A. B(x), P   Q, False, Q, False,  A, A A, A B, B,  , ,  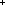 , ,  , Valtype(da;k), State(ds), (x , Valtype(da;k), State(ds), (x  l), ecl-trans-type(A), ecl-trans-tuple{i:l}(ds;da), S l), ecl-trans-type(A), ecl-trans-tuple{i:l}(ds;da), S  T, ecl-trans-state(v;L), Top, KindDeq, T, ecl-trans-state(v;L), Top, KindDeq,   x. t(x), f(x)?z, event-info(ds;da), x. t(x), f(x)?z, event-info(ds;da),  b, Prop, A & B, as @ bs, P & Q, b, Prop, A & B, as @ bs, P & Q,  x:A. B(x), True, x:A. B(x), True,  T, let a,b,c,d,e,f,g = u in v(a;b;c;d;e;f;g), let x,y,z = a in t(x;y;z), ecl-trans-a(v), ecl-trans-ks(v), ecl-trans-act(ds;da;A), {T}, SQType(T), P T, let a,b,c,d,e,f,g = u in v(a;b;c;d;e;f;g), let x,y,z = a in t(x;y;z), ecl-trans-a(v), ecl-trans-ks(v), ecl-trans-act(ds;da;A), {T}, SQType(T), P   Q, i Q, i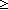 j, ||as||, S j, ||as||, S 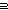 T, l1 T, l1  l2, a:A fp l2, a:A fp B(a), Id, Knd, B(a), Id, Knd,   b, deq-member(eq;x;L), Unit, if b b, deq-member(eq;x;L), Unit, if b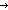 t else f fi, list_accum(x,a.f(x;a);y;l), t else f fi, list_accum(x,a.f(x;a);y;l),   x,y. t(x;y), ecl-trans-state-from(v;z;L), ecl-trans-init(v) x,y. t(x;y), ecl-trans-state-from(v;z;L), ecl-trans-init(v) |